Analysis of categorical data generally involves the use of data tables. A two-way table presents categorical data by counting the number of observations that fall into each group for two variables, one divided into rows and the other divided into columns. For example, suppose a survey was conducted of a group of 20 individuals, who were asked to identify their hair and eye color. A two-way table presenting the results might appear as follows:
Eye Color Hair Color Blue Green Brown Black Total ----------------------------------------------------- Blonde 2 1 2 1 6 Red 1 1 2 0 4 Brown 1 0 4 2 7 Black 1 0 2 0 3 ----------------------------------------------------- Total 5 2 10 3 20The totals for each category, also known as marginal distributions, provide the number of individuals in each row or column without accounting for the effect of the other variable (in the example above, the total number of individuals with blue eyes, regardless of hair color, is 5).
Since simple counts are often difficult to analyze, two-way tables are often converted into percentages. In the above example, there are 4 individuals with red hair. Since there were a total of 20 observations, this means that 20% of the individuals survered are redheads. One also might want to investigate the percentages within a given category -- of the 4 redheads, 2 (50%) have brown eyes, 1 (25%) has blue eyes, and 1 (25%) has green eyes.
For a more detailed example, consider the following dataset, "Weights of 1996 US Olympic Rowing Team." The first column gives the name of the rower, the second gives his event, and the third gives his weight. There are 8 different event categories, with weight given as numeric data.
Auth LW_double_sculls 154 Klepacki four 205 Beasley single_sculls 224 Koven eight 200 Brown eight 214 Mueller quad 215 Burden eight 195 Murphy eight 220 Carlucci LW_four 160 Murray four 205 Collins,D LW_four 155 Peterson,M pair 210 Collins,P eight 195 Peterson,S LW_double_sculls 160 Gailes quad 205 Pfaendtner LW_four 160 Hall four 195 Schnieder LW_four 158 Holland pair 195 Scott four 208 Honebein eight 200 Segaloff coxswain 121 Jamieson quad 210 Smith eight 207 Kaehler eight 210 Young quad 207
Data source: Team member biographies given on the NBC Olympic Web Site. Dataset available through the JSE Dataset Archive.
Descriptive Statistics Variable N Mean Median Tr Mean StDev SE Mean Weight 26 191.85 202.50 193.46 26.27 5.15 Variable Min Max Q1 Q3 Weight 121.00 224.00 160.00 210.00One might choose, based on this information, to divide the weight values into 4 groups, such as under 150 lbs, 150-175 lbs, 175-200 lbs, and over 200 lbs. Once the data has been categorized (the MINITAB "CODE" command may be used to perform this function), the MINITAB "TABLE" command will create two-way tables, as follows:
Rows: Event Columns: Weight_Class
<150 150-175 175-200 >200 All
LW_doubl 0 2 0 0 2
single_s 0 0 0 1 1
eight 0 0 4 4 8
LW_four 0 4 0 0 4
quad 0 0 0 4 4
four 0 0 1 3 4
pair 0 0 1 1 2
coxswain 1 0 0 0 1
All 1 6 6 13 26
Using the "ROWPERCENT" subcommand reproduces this table with the percentages of rowers in each
weight category by event:
Rows: Event Columns: Weight_Class
0 1 2 3 All
LW_doubl -- 100.00 -- -- 100.00
single_s -- -- -- 100.00 100.00
eight -- -- 50.00 50.00 100.00
LW_four -- 100.00 -- -- 100.00
quad -- -- -- 100.00 100.00
four -- -- 25.00 75.00 100.00
pair -- -- 50.00 50.00 100.00
coxswain 100.00 -- -- -- 100.00
All 3.85 23.08 23.08 50.00 100.00
These results indicate that half of all rowers are in the upper weight class, with the remainder
evenly divided between the two middle classes (with the exception of the coxswain, who is the only
team member in the lightest weight group). Similarly, the "COLPERCENT" subcommand provides the
percentage of rowers in each event category by weight.
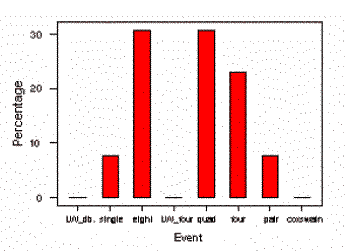
In addition to creating data tables, an analyst might want to create a graphical representation of categorical data using a bar graph. A bar graph representing the percentage of rowers in the heaviest weight category in each event is shown to the left.
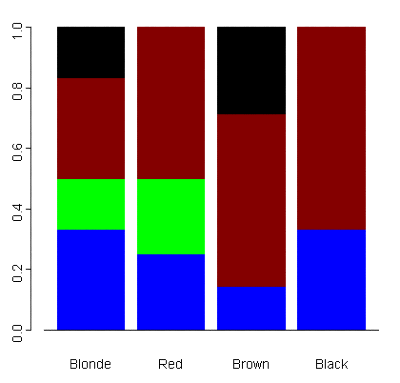
Another useful graphical tool for analyzing categorical data is a segmented bar graph. For the simple hair color/eye color example above, a segmented bar graph depicting the breakdown of eye color for each hair color appears to the right. The segments of each bar are color-coded to correspond to the appropriate eye color.