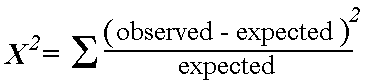 .
.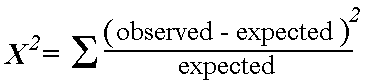 .
.Number of Sixes Number of Rolls 0 48 1 35 2 15 3 3The casino becomes suspicious of the gambler and wishes to determine whether the dice are fair. What do they conclude?
If a die is fair, we would expect the probability of rolling a 6 on any given toss to be 1/6. Assuming the 3 dice are independent (the roll of one die should not affect the roll of the others), we might assume that the number of sixes in three rolls is distributed Binomial(3,1/6). To determine whether the gambler's dice are fair, we may compare his results with the results expected under this distribution. The expected values for 0, 1, 2, and 3 sixes under the Binomial(3,1/6) distribution are the following:
Null Hypothesis:
p1 = P(roll 0 sixes) = P(X=0) = 0.58
p2 = P(roll 1 six) = P(X=1) = 0.345
p3 = P(roll 2 sixes) = P(X=2) = 0.07
p4 = P(roll 3 sixes) = P(X=3) = 0.005.
Since the gambler plays 100 times, the expected counts are the following:
Number of Sixes Expected Counts Observed Counts 0 58 48 1 34.5 35 2 7 15 3 0.5 3The two plots shown below provide a visual comparison of the expected and observed values:
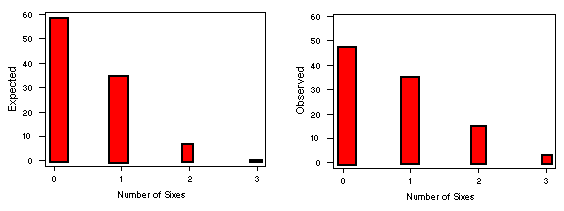
From these graphs, it is difficult to distinguish differences between the observed and expected counts. A visual representation of the differences is the chi-gram, which plots the observed - expected counts divided by the square root of the expected counts, as shown below:
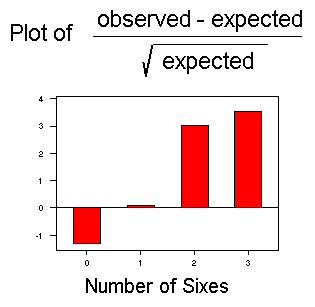
The chi-square statistic is the sum of the squares of the plotted values,
(48-58)²/58 + (35-34.5)²/58 + (15-7)²/7 + (3-0.5)²/0.5
= 1.72 + 0.007 + 9.14 + 12.5 = 23.367.
Given this statistic, are the observed values likely under the assumed model?
The standardized counts (observed - expected )/sqrt(expected) for k
possibilities are approximately normal, but they are not independent because
one of the counts is entirely determined by the sum of the others (since
the total of the observed and expected counts must sum to n). This
results in a loss of one degree of freedom, so it turns out the the distribution
of the chi-square test statistic based on k counts is approximately
the chi-square distribution with m = k-1 degrees of freedom,
denoted ![]() (k-1).
(k-1).
Let p1, p2, ..., pk denote the
probabilities hypothesized for k possible outcomes. In n
independent trials, we let Y1, Y2, ..., Yk
denote the observed counts of each outcome which are to be compared to
the expected counts np1, np2, ..., npk.
The chi-square test statistic is qk-1 =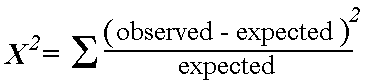
= (Y1 - np1)² + (Y2 - np2)² + ... + (Yk - npk)² ---------- ---------- -------- np1 np2 npkReject H0 if this value exceeds the upper
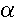 critical value of the
critical value of the 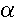 is the desired
level of significance.
is the desired
level of significance.
Given this information, the casino asked the gambler to take his dice (and his business) elsewhere.
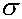 y2 = np(1-p).
y2 = np(1-p).
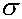 y
has an approximately Normal(0,1) distribution for large values of n.
Then Z² is approximately
y
has an approximately Normal(0,1) distribution for large values of n.
Then Z² is approximately Suppose the random variable Y1 has a Bin(n,p1) distribution, and let Y2 = n - Y1 and p2 = 1 - p1.
Then Z² = (Y1 - np1)² ---------- np1(1-p1) = (Y1 - np1)²(1 - p1) + (Y1 - np1)²(p1) --------------------------------------- np1(1-p1) = (Y1 - np1)² + (Y1 - np1)² ---------- ---------- np1 n(1-p1)Since (Y1 - np1)² = (n - Y2 - n + np2)² = (Y2 - np2)²,
we have Z² = (Y1 - np1)² + (Y2 - np2)² ---------- ---------- np1 np2where Z² has a chi-square distribution with 1 degree of freedom. If the observed values Y1 and Y2 are close to their expected values np1 and np2, then the calculated value Z² will be close to zero. If not, Z² will be large.
In general, for k random variables Yi, i = 1, 2,..., k, with corresponding expected values npi, a statistic measuring the "closeness" of the observations to their expectations is the sum
(Y1 - np1)² + (Y2 - np2)² + ... + (Yk - npk)² ---------- ---------- -------- np1 np2 npkwhich has a chi-square distribution with k-1 degrees of freedom.
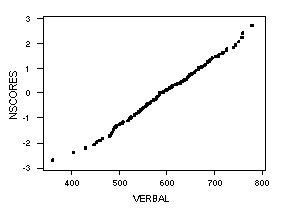
To compute a chi-square test statistic, I first standardized the verbal scores data by subtracting the sample mean and dividing by the sample standard deviation. Since these are estimated parameters, my value for d in the test statistic will be equal to two. The 200 standardized observations are the following:
[1] -2.11801 -2.69073 0.76066 1.04702 0.91138 -0.09842 0.23316 1.04702 0.65516 0.77573 [11] -0.53549 -1.39457 -0.58071 0.77573 -0.58071 0.47430 0.05230 -2.25365 -0.21899 -0.98764 [21] -0.30942 -0.38478 0.23316 1.12238 1.45396 0.05230 -0.67114 -1.25893 1.12238 0.41402 [31] 1.19774 -0.58071 0.50445 1.92118 -0.67114 0.05230 0.36880 -0.23406 -0.73142 0.77573 [41] -1.54529 1.55946 0.03723 0.21809 0.21809 -0.71635 -1.39457 -1.81658 0.98674 -0.85200 [51] 0.17287 0.64009 0.33866 -3.14288 1.19774 0.47430 1.92118 -0.17378 0.77573 0.76066 [61] 0.64009 0.91138 1.33338 -0.17378 0.33866 -0.67114 -0.53549 -0.29435 -0.95750 0.77573 [71] 0.47430 -0.03813 -0.53549 0.29344 0.36880 0.21809 0.12766 1.31831 2.26782 0.27837 [81] -1.24386 1.83075 1.04702 1.58960 0.03723 0.33866 -0.30942 -0.58071 -0.71635 -0.15870 [91] -0.03813 0.83602 0.27837 0.77573 -0.03813 -1.00271 -0.85200 -0.73142 -0.29435 0.68531 [101] -0.09842 -0.71635 0.23316 -1.15343 1.04702 -0.71635 -2.02758 1.27310 0.05230 0.27837 [111] 1.72524 -0.67114 -0.71635 -0.71635 0.68531 1.86089 0.91138 -1.40965 0.09751 -0.53549 [121] 0.64009 -0.06827 -0.53549 0.36880 -2.40437 1.99653 -1.12329 0.41402 1.12238 -0.42999 [131] -0.61085 0.91138 -0.38478 -1.33429 -0.47521 0.91138 0.76066 -0.09842 -0.44506 -1.24386 [141] -0.35463 -0.44506 -0.42999 0.23316 -0.21899 0.91138 -0.23406 0.09751 0.50445 -0.58071 [151] -0.98764 -1.12329 0.23316 -0.95750 1.48410 -0.17378 -1.39457 -0.85200 -0.58071 1.48410 [161] -0.42999 1.19774 0.54966 -1.12329 1.45396 -0.30942 0.18794 -0.86707 -0.38478 -1.00271 [171] -0.09842 -1.42472 1.31831 -0.71635 -1.83165 2.26782 -0.00799 -1.12329 -0.42999 1.04702 [181] -1.86179 -1.10821 0.41402 1.31831 0.64009 1.12238 0.48937 -0.00799 -0.30942 -0.38478 [191] 1.72524 -1.10821 -0.38478 0.41402 -0.03813 -1.68093 -1.86179 0.33866 2.20754 0.91138I chose to divide the observations into 10 bins, as follows:
Bin Observed Counts (< -2.0) 6 (-2.0, -1.5) 6 (-1.5, -1.0) 18 (-1.0, -0.5) 33 (-0.5, 0.0) 38 (0.0, 0.5) 38 (0.5, 1.0) 28 (1.0, 1.5) 21 (1.5, 2.0) 9 (> 2.0) 3The corresponding standard normal probabilities and the expected number of observations (with n=200) are the following:
Bin Normal Prob. Expected Counts Observed - Expected Chi-Value (< -2.0) 0.023 4.6 1.4 0.65 (-2.0, -1.5) 0.044 8.8 -2.8 -0.94 (-1.5, -1.0) 0.092 18.4 -0.4 -0.09 (-1.0, -0.5) 0.150 30.0 3.0 0.55 (-0.5, 0.0) 0.191 38.2 -0.2 -0.03 (0.0, 0.5) 0.191 38.2 -0.2 -0.03 (0.5, 1.0) 0.150 30.0 -2.0 -0.36 (1.0, 1.5) 0.092 18.4 2.6 0.61 (1.5, 2.0) 0.044 8.8 0.2 0.07 (> 2.0) 0.023 4.6 -1.6 -0.75The chi-square statistic is the sum of the squares of the values in the last column, and is equal to 2.69.
Since the data are divided into 10 bins and we have estimated two parameters, the calculated value may be tested against the chi-square distribution with 10 -1 -2 = 7 degrees of freedom. For this distribution, the critical value for the 0.05 significance level is 14.07. Since 2.69 < 14.07, we do not reject the null hypothesis that the data are normally distributed.