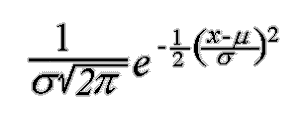
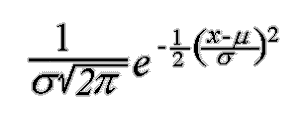
 The Standard
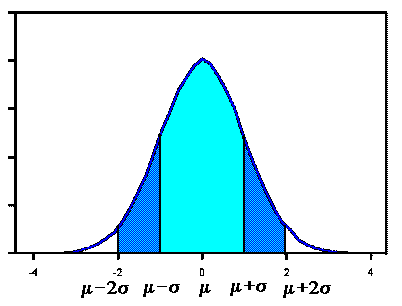
Normal curve, shown here, has mean 0 and standard deviation 1. If a dataset follows
a normal distribution, then about 68% of the observations will fall
within
The Standard
Normal curve, shown here, has mean 0 and standard deviation 1. If a dataset follows
a normal distribution, then about 68% of the observations will fall
within ![]() of the mean
of the mean ![]() , which in this case is with
the interval (-1,1). About 95% of the observations will fall within 2 standard deviations
of the mean, which is the interval (-2,2) for the standard normal, and about 99.7%
of the observations will fall within 3 standard deviations of the mean, which
corresponds to the interval (-3,3) in this case. Although it may appear as if a
normal distribution does not include any values beyond a certain interval, the density
is actually positive for all values,
, which in this case is with
the interval (-1,1). About 95% of the observations will fall within 2 standard deviations
of the mean, which is the interval (-2,2) for the standard normal, and about 99.7%
of the observations will fall within 3 standard deviations of the mean, which
corresponds to the interval (-3,3) in this case. Although it may appear as if a
normal distribution does not include any values beyond a certain interval, the density
is actually positive for all values, 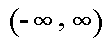 .
Data from any normal distribution may be transformed into data following the standard normal
distribution by subtracting the mean
.
Data from any normal distribution may be transformed into data following the standard normal
distribution by subtracting the mean ![]() and dividing
by the standard deviation
and dividing
by the standard deviation ![]() .
.
Variable N Mean Median Tr Mean StDev SE Mean BODY TEMP 130 98.249 98.300 98.253 0.733 0.064 Variable Min Max Q1 Q3 BODY TEMP 96.300 100.800 97.800 98.700The spread of the data is very small, as might be expected.
The normality of the data may be evaluated by using the MINITAB "NSCORES" command to calculate the normal scores for the data, then plotting the observed data against the normal quantile values. For the first 10 sorted observations, the table below displays the original temperature values in the first column, standardized values in the second column (calculated by subtracting the mean 98.249 and dividing by the standard deviation 0.733), and corresponding normal scores in the third column.
96.3 -2.65894 -2.58163 96.4 -2.52251 -2.24352 96.7 -2.11323 -1.98066 96.7 -2.11323 -1.98066 96.8 -1.97681 -1.80820 96.9 -1.84038 -1.71725 97.0 -1.70396 -1.63847 97.1 -1.56753 -1.50561 97.1 -1.56753 -1.50561 97.1 -1.56753 -1.50561
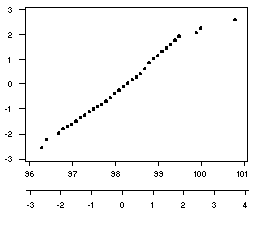 The standardized values in the second column and the corresponding normal quantile scores
are very similar, indicating that the temperature data seem to fit a normal distribution.
The plot of these columns, with the temperature values on the horizontal axis and the
normal quantile scores on the vertical axis, is shown to the right (the two scales in the
horizontal axis provide original and standardized values).
This plot indicates that the data appear to follow a normal
distribution, with only the three largest values deviating from a straight diagonal line.
The standardized values in the second column and the corresponding normal quantile scores
are very similar, indicating that the temperature data seem to fit a normal distribution.
The plot of these columns, with the temperature values on the horizontal axis and the
normal quantile scores on the vertical axis, is shown to the right (the two scales in the
horizontal axis provide original and standardized values).
This plot indicates that the data appear to follow a normal
distribution, with only the three largest values deviating from a straight diagonal line.
Data source: Derived from Mackowiak, P.A., Wasserman, S.S., and Levine, M.M. (1992), "A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and Other Legacies of Carl Reinhold August Wunderlick," Journal of the American Medical Association, 268, 1578-1580. Dataset available through the JSE Dataset Archive.
To compute the probability of observing values within an interval, one must subtract the cumulative probability for the smaller value from the cumulative probability for the larger value. Suppose, for example, we are interested in the probability of observing values within the standard normal interval (0,0.5). The probability of observing a value less than or equal to 0.5 (from Table A) is equal to 0.6915, and the probability of observing a value less than or equal to 0 is 0.5. The probability of the normal interval (0, 0.5) is equal to 0.6915 - 0.5 = 0.1915.
VALUE Z-VALUE CDF 96.7 -2.11302 0.017299 98.0 -0.33993 0.366955 98.3 0.06924 0.527603 98.5 0.34203 0.633835 98.8 0.75120 0.773735 99.9 2.25151 0.987823The values below the observed mean, 98.249, have negative standardized values and relative frequencies less than 0.5, while values above the mean have positive standardized values and relative frequencies greater than 0.5. Notice that the probability of observing a value smaller than 96.7 is very small, as is the probability of observing a value greater than 99.9 (this probability is 1- (the probability of observing a value less than 99.9) = 1-0.9878 = 0.0122). Both of these values lie outside of the (-2,2) interval, which includes 95% of the data in a standard normal distribution.