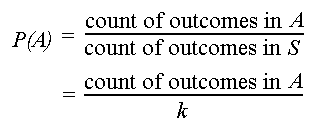
The sample space S for a probability model is the set of all possible outcomes.
For example, suppose there are 5 marbles in a bowl. One is red, one is blue, one is yellow, one is green, and one is purple. If one marble is to be picked at random from the bowl, the sample space possible outcomes S = {red, blue, yellow, green, purple}. If 3 of the marbles are red and 2 are blue, then the sample space S = {red, blue}, since only two possible color outcomes be possible. If, instead, two marbles are picked from a bowl with 3 red marbles and 2 blue marbles, then the sample space S = {(2 red), (2 blue), (1 red and 1 blue)}, the set of all possible outcomes.
An event A is a subset of the sample space S.
Suppose there are 3 red marbles and 2 blue marbles in a bowl. If an individual picks three marbles, one at a time, from the bowl, the event "pick 2 red marbles" can be achieved in 3 ways, so the set of outcomes A = {(red,red, blue),(red, blue,red), (blue, red,red)}. The sample space for picking three marbles, one at a time, is all of the possible ordered combinations of three marbles, S = {(red, red, red), (red, red, blue), (red, blue, red), (blue, red, red), (blue, blue, red), (blue, red, blue), (red, blue, blue)}. Since there are only 2 blue marbles, it is impossible to achieve the event {blue, blue,blue}.
A probability is a numerical value assigned to a given event A. The probability of an event is written P(A), and describes the long-run relative frequency of the event. The first two basic rules of probability are the following:
Suppose five marbles, each of a different color, are placed in a bowl. The sample space for choosing one marble, from above, is S = {red, blue, yellow, green, purple}. Since one of these must be selected, the probability of choosing any marble is equal to the probability of the sample space S = 1. Suppose the event of interest is choosing the purple marble, A = {purple}. If it is equally likely that any one marble will be selected, then the probability of choosing the purple marble, P(A) = 1/5. In general, the following formula describes the calculation of probabilities for equally likely outcomes:
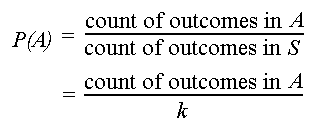
If two events have no outcomes in common, then they are called disjoint. For example, the possible outcomes of picking a single marble are disjoint: only one color is possible on each pick. The addition of probabilities for disjoint events is the third basic rule of probability:
The chance of any (one or more) of two or more events occurring is called the union of the events. The probability of the union of disjoint events is the sum of their individual probabilities.
For example, the probability of drawing either a purple, red, or green marble from a bowl of five differently colored marbles is the sum of the probabilities of drawing any of these marbles: 1/5 + 1/5 + 1/5 = 3/5.
If there are three red marbles and two blue marbles, then the probability of drawing any red marble is the number of outcomes in the event " red," which is equal to three, divided by the total number of outcomes, 5, or 3/5 = 0.6. The sample space is this case is {red, blue}, which must have total probability equal to 1, so the probability of drawing a blue marble is equal to 2/5 = 0.4. The event of drawing a blue marble does not occur if a red marble is chosen, so the event A = "blue" is called the complement Ac of the event "red." Since an event and its complement together form the entire sample space S, the probability of an event A is equal to the probability of the sample space S, minus the probability of Ac, as follows:
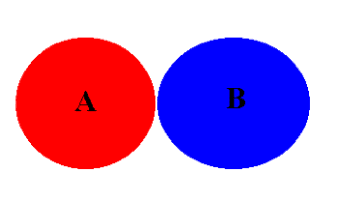 In the Venn diagram to the right, events A
and B are disjoint. Suppose, for example, event A is drawing a
red marble from a bowl of five differently colored marbles, and
event B is drawing a blue marble. These events cannot
both occur, so there is no overlapping area.
In the Venn diagram to the right, events A
and B are disjoint. Suppose, for example, event A is drawing a
red marble from a bowl of five differently colored marbles, and
event B is drawing a blue marble. These events cannot
both occur, so there is no overlapping area.
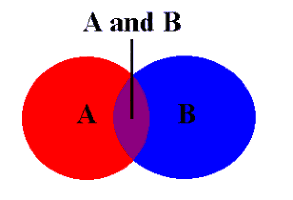 In the Venn diagram on the left,
events A and B are not disjoint. This means that it is possible for
both events to occur, and the overlapping area represents this possibility. Suppose,
for instance, there are 3 red marbles and two
blue marbles in a bowl. Two marbles are to be drawn from the
bowl, one after the other. After the first draw, the marble drawn is returned to the bowl.
Define event A to be drawing a red marble from the
bowl on the first draw, and define event B to be drawing a
blue marble on the second draw. The occurence of event
A is represented by the red area, the occurence of event B
is represented by the blue area, the occurence of both events
is represented by the overlapping area (also known as the intersection of the two events),
and the occurence of either event is represented by the entire colored area (also
known as the union of the two events).
In the Venn diagram on the left,
events A and B are not disjoint. This means that it is possible for
both events to occur, and the overlapping area represents this possibility. Suppose,
for instance, there are 3 red marbles and two
blue marbles in a bowl. Two marbles are to be drawn from the
bowl, one after the other. After the first draw, the marble drawn is returned to the bowl.
Define event A to be drawing a red marble from the
bowl on the first draw, and define event B to be drawing a
blue marble on the second draw. The occurence of event
A is represented by the red area, the occurence of event B
is represented by the blue area, the occurence of both events
is represented by the overlapping area (also known as the intersection of the two events),
and the occurence of either event is represented by the entire colored area (also
known as the union of the two events).
The chance of all of two or more events occurring is called the intersection of events. For independent events, the probability of the intersection of two or more events is the product of the probabilities.
In the case of two coin flips, for example, the probability of observing two heads is 1/2*1/2 = 1/4. Similarly, the probability of observing four heads on four coin flips is 1/2*1/2*1/2*1/2 = 1/16.
If two events A and B are not disjoint, then the probability of their union (the event that A or B occurs) is equal to the sum of their probabilities minus the sum of their intersection.
In the example corresponding to the second Venn diagram above, we know that the probability
of drawing a red marble on the first draw (event A) is
equal to 3/5, and the probability of drawing a blue marble on
the second draw (event B) is equal to 2/5. Since events A and B are
independent, the probability of the intersection of A and B, P(A and B), equals the
product P(A)*P(B) = 3/5*2/5 = 6/25. The probability of the union of A and
B, P(A or B), is equal to
P(A) + P(B) - P(A and B) = 3/5 + 2/5 - 6/25 = 1 - 6/25 = 19/25 = 0.76.
For another example, consider tossing two coins. The probability of a head on any toss is equal to 1/2. Since the tosses are independent, the probability of a head on both tosses (the intersection) is equal to 1/2*1/2 = 1/4. The probability of a head on either toss (the union) is equal to the sum of the probabilities of a head on each toss minus the probability of the intersection, 1/2 + 1/2 - 1/4 = 3/4.
Note: Disjoint events are not independent. In the marble example, consider drawing one marble from the bowl of five, where each marble is a different color. Suppose the event of interest, event A, is drawing a blue marble. The probability of drawing this marble is 1/5. Suppose event B is drawing a green marble. These events are disjoint, since event B cannot occur if event A occurs. Obviously, they are not independent, since the outcome of event A directly affects the outcome of event B. If, instead, two marbles were to be drawn from the bowl, with the first marble replaced before the second marble was drawn, then the event of drawing a blue marble on the first draw would not affect the outcome of the second draw. The event of drawing a green marble on the second draw would be independent of the event of drawing a blue marble on the first draw, so the probability of both events occurring would be the product of the probabilities of each event, 1/5*1/5 = 1/25.
The probability of the intersection of two or events which are not independent is determined using conditional probabilities.
For some more definitions and examples, see the probability index in Valerie J. Easton and John H. McColl's Statistics Glossary v1.1.