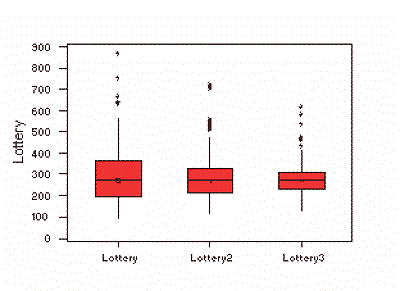
These MINITAB boxplots represent lottery payoffs
for winning numbers for three time periods (May 1975-March 1976, November 1976-September 1977, and
December 1980-September 1981).
The median for each dataset is indicated by the black center line, and the first and third quartiles are the edges of the red area, which is known as the inter-quartile range (IQR). The extreme values (within 1.5 times the inter-quartile range from the upper or lower quartile) are the ends of the lines extending from the IQR. Points at a greater distance from the median than 1.5 times the IQR are plotted individually as asterisks. These points represent potential outliers.
In this example, the three boxplots have nearly identical median values. The IQR is decreasing from one time period to the next, indicating reduced variability of payoffs in the second and third periods. In addition, the extreme values are closer to the median in the later time periods.
The datasets are available in S-Plus 3.3, where they are republished by permission of the New Jersey State Lottery Commission.