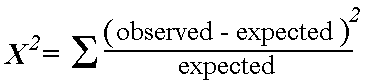
Grade Goals | 4 5 6 Total --------------------------------- Grades | 49 50 69 168 Popular | 24 36 38 98 Sports | 19 22 28 69 --------------------------------- Total | 92 108 135 335To investigate possible differences among the students' choices by grade, it is useful to compute the column percentages for each choice, as follows:
Grade Goals | 4 5 6 --------------------------- Grades | 53 46 51 Popular | 26 33 28 Sports | 21 20 21 --------------------------- Total | 100 100 100There is error in the second column (the percentages sum to 99, not 100) due to rounding. From the appearance of the column percentages, it does not appear that there is much of a variation in preference across the three grades.
Data source: Chase, M.A and Dummer, G.M. (1992), "The Role of Sports as a Social Determinant for Children," Research Quarterly for Exercise and Sport, 63, 418-424. Dataset available through the Statlib Data and Story Library (DASL).
The chi-square test is based on a test statistic that measures the divergence of the observed data from the values that would be expected under the null hypothesis of no association. This requires calculation of the expected values based on the data. The expected value for each cell in a two-way table is equal to (row total*column total)/n, where n is the total number of observations included in the table.
Original Table Expected Values Grade Grade Goals | 4 5 6 Total Goals | 4 5 6 --------------------------------- --------------------------- Grades | 49 50 69 168 Grades | 46.1 54.2 67.7 Popular | 24 36 38 98 Popular | 26.9 31.6 39.5 Sports | 19 22 28 69 Sports | 18.9 22.2 27.8 --------------------------------- Total | 92 108 135 335The first cell in the expected values table, Grade 4 with "grades" chosen to be most important, is calculated to be 168*92/335 = 46.1, for example.
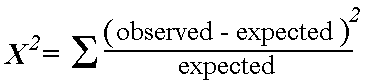
The distribution of the statistic X2 is chi-square
with (r-1)(c-1) degrees of freedom, where r represents
the number of rows in the two-way table and c represents the
number of columns. The distribution is denoted ![]() (df), where
df is the number of degrees of freedom.
(df), where
df is the number of degrees of freedom.
The chi-square distribution is defined for all positive values. The P-value
for the chi-square test is P(![]() >X²), the
probability of observing a value at least as extreme as the test statistic
for a chi-square distribution with (r-1)(c-1) degrees of
freedom.
>X²), the
probability of observing a value at least as extreme as the test statistic
for a chi-square distribution with (r-1)(c-1) degrees of
freedom.
A two-way table for student goals and school area appears as follows:
School Area Goals | Rural Suburban Urban Total -------------------------------------------- Grades | 57 87 24 168 Popular | 50 42 6 98 Sports | 42 22 5 69 -------------------------------------------- Total | 149 151 35 335The corresponding column percentages are the following:
School Area Goals | Rural Suburban Urban ----------------------------------- Grades | 38 58 69 Popular | 34 28 17 Sports | 28 14 14 ----------------------------------- Total | 100 100 100Barplots comparing the percentages of students' choices by school area appear below:
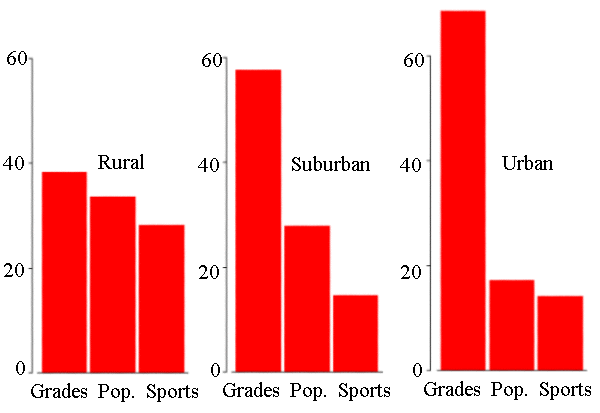
From the table and corresponding graphs, it appears that the emphasis on grades increases as the school areas become more urban, while the emphasis on popularity decreases. Is this association significant?
Using the MINITAB "CHIS" command to perform a chi-square test on the tabular data gives the following results:
Chi-Square Test
Expected counts are printed below observed counts
Rural Suburban Urban Total
1 57 87 24 168
74.72 75.73 17.55
2 50 42 6 98
43.59 44.17 10.24
3 42 22 5 69
30.69 31.10 7.21
Total 149 151 35 335
Chi-Sq = 4.203 + 1.679 + 2.369 +
0.943 + 0.107 + 1.755 +
4.168 + 2.663 + 0.677 = 18.564
DF = 4, P-Value = 0.001
The P-value is highly significant, indicating that some association between the variables
is present. We can conclude that the urban students' increased emphasis on grades is not due to
random variation.
Data source: Chase, M.A and Dummer, G.M. (1992), "The Role of Sports as a Social Determinant for Children," Research Quarterly for Exercise and Sport, 63, 418-424. Dataset available through the Statlib Data and Story Library (DASL).