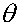 .
Often, this parameter is the population mean
.
Often, this parameter is the population mean  , which is
estimated through the
, which is
estimated through the
The level C of a confidence interval gives the probability
that the interval produced by the method employed includes the true value
of the parameter 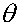 .
.
Example
Suppose a student measuring the boiling temperature of a certain liquid observes the readings (in degrees Celsius) 102.5, 101.7, 103.1, 100.9, 100.5, and 102.2 on 6 different samples of the liquid. He calculates the sample mean to be 101.82. If he knows that the standard deviation for this procedure is 1.2 degrees, what is the confidence interval for the population mean at a 95% confidence level?
In other words, the student wishes to estimate the true mean boiling temperature
of the liquid using the results of his measurements. If the
measurements follow a normal distribution, then the sample mean will
have the distribution
N( ,
,![]() ). Since the sample size is 6, the standard
deviation of the sample mean is equal to 1.2/sqrt(6) = 0.49.
). Since the sample size is 6, the standard
deviation of the sample mean is equal to 1.2/sqrt(6) = 0.49.
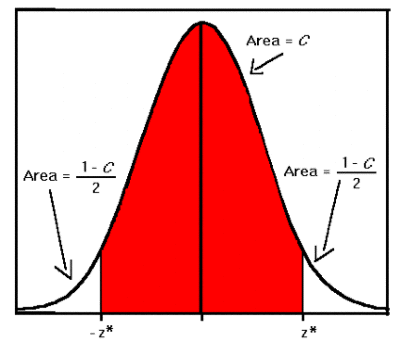 The selection of a confidence level for an interval determines the probability
that the confidence interval produced will contain the true parameter value.
Common choices for the confidence level C are 0.90, 0.95, and 0.99.
These levels correspond to percentages of the area of the normal density curve.
For example, a 95% confidence interval covers 95% of the
normal curve -- the probability of observing a value outside of
this area is less than 0.05. Because the normal curve is symmetric,
half of the area is in the left tail of the curve, and the other
half of the area is in the right tail of the curve. As shown in the
diagram to the right, for a confidence interval with level C, the area
in each tail of the curve is equal to (1-C)/2. For a 95% confidence
interval, the area in each tail is equal to 0.05/2 = 0.025.
The selection of a confidence level for an interval determines the probability
that the confidence interval produced will contain the true parameter value.
Common choices for the confidence level C are 0.90, 0.95, and 0.99.
These levels correspond to percentages of the area of the normal density curve.
For example, a 95% confidence interval covers 95% of the
normal curve -- the probability of observing a value outside of
this area is less than 0.05. Because the normal curve is symmetric,
half of the area is in the left tail of the curve, and the other
half of the area is in the right tail of the curve. As shown in the
diagram to the right, for a confidence interval with level C, the area
in each tail of the curve is equal to (1-C)/2. For a 95% confidence
interval, the area in each tail is equal to 0.05/2 = 0.025.
The value z* representing the point on the standard normal density curve such that the probability of observing a value greater than z* is equal to p is known as the upper p critical value of the standard normal distribution. For example, if p = 0.025, the value z* such that P(Z > z*) = 0.025, or P(Z < z*) = 0.975, is equal to 1.96. For a confidence interval with level C, the value p is equal to (1-C)/2. A 95% confidence interval for the standard normal distribution, then, is the interval (-1.96, 1.96), since 95% of the area under the curve falls within this interval.
Confidence Intervals for Unknown Mean and Known Standard Deviation
For a population with unknown mean and known standard deviation
and known standard deviation
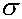 , a confidence interval for the population mean,
based on a simple random sample (SRS) of size n,
is
, a confidence interval for the population mean,
based on a simple random sample (SRS) of size n,
is Note: This interval is only exact when the population distribution is normal. For large samples from other population distributions, the interval is approximately correct by the Central Limit Theorem.
In the example above, the student calculated the sample mean of the boiling temperatures to be 101.82, with standard deviation 0.49. The critical value for a 95% confidence interval is 1.96, where (1-0.95)/2 = 0.025. A 95% confidence interval for the unknown mean
 is ((101.82 - (1.96*0.49)), (101.82 + (1.96*0.49))) = (101.82 - 0.96, 101.82 + 0.96) =
(100.86, 102.78).
is ((101.82 - (1.96*0.49)), (101.82 + (1.96*0.49))) = (101.82 - 0.96, 101.82 + 0.96) =
(100.86, 102.78).
As the level of confidence decreases, the size of the corresponding interval will decrease. Suppose the student was interested in a 90% confidence interval for the boiling temperature. In this case, C = 0.90, and (1-C)/2 = 0.05. The critical value z* for this level is equal to 1.645, so the 90% confidence interval is ((101.82 - (1.645*0.49)), (101.82 + (1.645*0.49))) = (101.82 - 0.81, 101.82 + 0.81) = (101.01, 102.63)
An increase in sample size will decrease the length of the confidence interval without reducing the level of confidence. This is because the standard deviation decreases as n increases. The margin of error m of a confidence interval is defined to be the value added or subtracted from the sample mean which determines the length of the interval: m = z*
Suppose in the example above, the student wishes to have a margin of error equal to 0.5 with 95% confidence. Substituting the appropriate values into the expression for m and solving for n gives the calculation n = (1.96*1.2/0.5)² = (2.35/0.5)² = 4.7² = 22.09. To achieve a 95% confidence interval for the mean boiling point with total length less than 1 degree, the student will have to take 23 measurements.
Confidence Intervals for Unknown Mean and Unknown Standard Deviation
In most practical research, the standard deviation for the population of interest is not known. In this case, the standard deviation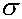 is replaced by
the estimated standard deviation s, also known as
the standard error. Since the standard error is an estimate for the true value of
the standard deviation, the distribution of the sample mean
is replaced by
the estimated standard deviation s, also known as
the standard error. Since the standard error is an estimate for the true value of
the standard deviation, the distribution of the sample mean
 and standard deviation
and standard deviation
 and standard deviation
and standard deviation
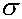 for large n.
for large n.
For a population with unknown mean  and unknown standard
deviation, a confidence interval for the population mean,
based on a simple random sample (SRS) of size n,
is
and unknown standard
deviation, a confidence interval for the population mean,
based on a simple random sample (SRS) of size n,
is ![]() +
t*
+
t*![]() ,
where t* is the upper (1-C)/2 critical value for the t
distribution with n-1 degrees of freedom, t(n-1).
,
where t* is the upper (1-C)/2 critical value for the t
distribution with n-1 degrees of freedom, t(n-1).
Example
The dataset "Normal Body Temperature, Gender, and Heart Rate" contains 130 observations of body temperature, along with the gender of each individual and his or her heart rate. Using the MINITAB "DESCRIBE" command provides the following information:
Descriptive Statistics Variable N Mean Median Tr Mean StDev SE Mean TEMP 130 98.249 98.300 98.253 0.733 0.064 Variable Min Max Q1 Q3 TEMP 96.300 100.800 97.800 98.700To find a 95% confidence interval for the mean based on the sample mean 98.249 and sample standard deviation 0.733, first find the 0.025 critical value t* for 129 degrees of freedom. This value is approximately 1.962, the critical value for 100 degrees of freedom (found in Table E in Moore and McCabe). The estimated standard deviation for the sample mean is 0.733/sqrt(130) = 0.064, the value provided in the SE MEAN column of the MINITAB descriptive statistics. A 95% confidence interval, then, is approximately ((98.249 - 1.962*0.064), (98.249 + 1.962*0.064)) = (98.249 - 0.126, 98.249+ 0.126) = (98.123, 98.375).
For a more precise (and more simply achieved) result, the MINITAB "TINTERVAL" command, written as follows, gives an exact 95% confidence interval for 129 degrees of freedom:
MTB > tinterval 95 c1 Confidence Intervals Variable N Mean StDev SE Mean 95.0 % CI TEMP 130 98.2492 0.7332 0.0643 ( 98.1220, 98.3765)According to these results, the usual assumed normal body temperature of 98.6 degrees Fahrenheit is not within a 95% confidence interval for the mean.
Data source: Data presented in Mackowiak, P.A., Wasserman, S.S., and Levine, M.M. (1992), "A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and Other Legacies of Carl Reinhold August Wunderlich," Journal of the American Medical Association, 268, 1578-1580. Dataset available through the JSE Dataset Archive.
For some more definitions and examples, see the confidence interval index in Valerie J. Easton and John H. McColl's Statistics Glossary v1.1.