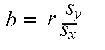 .
.Because the least-squares regression line will always pass through the means of x and y, the regression line may be entirely described by the means, standard deviations, and correlation of the two variables under investigation.
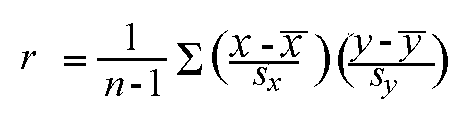
The correlation coefficient always takes a value between -1 and 1, with 1 or -1 indicating perfect correlation (all points would lie along a straight line in this case). A positive correlation indicates a positive association between the variables (increasing values in one variable correspond to increasing values in the other variable), while a negative correlation indicates a negative association between the variables (increasing values is one variable correspond to decreasing values in the other variable). A correlation value close to 0 indicates no association between the variables.
Since the formula for calculating the correlation coefficient standardizes the variables, changes in scale or units of measurement will not affect its value. For this reason, the correlation coefficient is often more useful than a graphical depiction in determining the strength of the association between two variables.
The correlation coefficient also relates directly to the regression line Y = a + bX
for any two variables, where 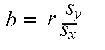 .
.
Because the least-squares regression line will always pass through the means of x and y, the regression line may be entirely described by the
means, standard deviations, and correlation of the two variables under investigation.
For some good examples of studies using correlation, see the correlation index in the Statlib Data and Story Library (DASL).