Linear Regression
Linear regression attempts to model the relationship between two variables by fitting a linear
equation to observed data. One variable is considered to be an explanatory variable, and the
other is considered to be a dependent variable. For example, a modeler might want to relate
the weights of individuals to their heights using a linear regression model.
Before attempting to fit a linear model to observed data, a modeler should first determine
whether or not there is a relationship between the variables of interest. This does not
necessarily imply that one variable causes the other (for example, higher SAT scores do
not cause higher college grades), but that there is some significant association between
the two variables. A scatterplot can be a helpful tool in
determining the strength of the relationship between two variables. If there appears to be no
association between the proposed explanatory and dependent variables (i.e., the scatterplot does
not indicate any increasing or decreasing trends), then fitting a linear regression model to
the data probably will not provide a useful model. A valuable numerical measure of association
between two variables is the correlation coefficient, which is a value
between -1 and 1 indicating the strength of the association of the observed data for the
two variables.
A linear regression line has an equation of the form Y = a + bX,
where X is the explanatory variable and Y is the dependent variable.
The slope of the line is b, and a is the intercept (the value of
y when x = 0).
Least-Squares Regression
The most common method for fitting a regression line is the method of least-squares. This method
calculates the best-fitting line for the observed data by minimizing the sum of the squares of the
vertical deviations from each data point to the line (if a point lies on the fitted line exactly,
then its vertical deviation is 0). Because the deviations are first squared, then summed, there
are no cancellations between positive and negative values.
Example
The dataset "Televisions, Physicians, and Life Expectancy" contains, among other variables,
the number of people per television set and the number of people per physician for 40 countries.
Since both variables probably reflect the level of wealth in each country, it is reasonable to
assume that there is some positive association between them. After removing 8 countries with
missing values from the dataset, the remaining 32 countries have a correlation coefficient
of 0.852 for number of people per television set and number of people per physician.
The r² value is 0.726 (the square of the correlation coefficient), indicating that
72.6% of the variation in one variable may be explained by the other. (Note: see
correlation for more detail.) Suppose we choose to consider number
of people per television set as the explanatory variable, and number of people per physician as
the dependent variable. Using the MINITAB "REGRESS" command gives the following results:
The regression equation is People.Phys. = 1019 + 56.2 People.Tel.
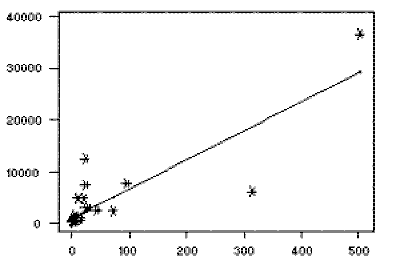 To view the fit of the model to the observed data, one may plot the computed regression line over
the actual data points to evaluate the results. For this example, the plot appears to the right,
with number of individuals per television set (the explanatory variable) on the x-axis and number
of individuals per physician (the dependent variable) on the y-axis. While most of the data points
are clustered towards the lower left corner of the plot (indicating relatively few individuals
per television set and per physician), there are a few points which lie far away from the main
cluster of the data. These points are known as outliers, and depending on their
location may have a major impact on the regression line (see below).
To view the fit of the model to the observed data, one may plot the computed regression line over
the actual data points to evaluate the results. For this example, the plot appears to the right,
with number of individuals per television set (the explanatory variable) on the x-axis and number
of individuals per physician (the dependent variable) on the y-axis. While most of the data points
are clustered towards the lower left corner of the plot (indicating relatively few individuals
per television set and per physician), there are a few points which lie far away from the main
cluster of the data. These points are known as outliers, and depending on their
location may have a major impact on the regression line (see below).
Data source: The World Almanac and Book of Facts 1993 (1993), New York: Pharos Books.
Dataset available through the
JSE Dataset Archive.
Outliers and Influential Observations
After a regression line has been computed for a group of data, a point which lies far from the line
(and thus has a large residual value) is known as an outlier. Such points may
represent erroneous data, or may indicate a poorly fitting regression line. If a point lies far
from the other data in the horizontal direction, it is known as an influential
observation. The reason for this distinction is that these points have may have a
significant impact on the slope of the regression line. Notice, in the above example, the effect
of removing the observation in the upper right corner of the plot:
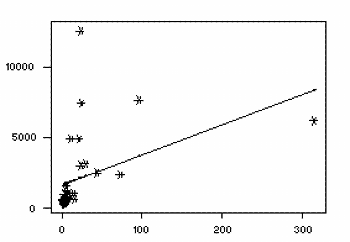 With this influential observation removed, the regression equation is
now
With this influential observation removed, the regression equation is
now
People.Phys = 1650 + 21.3 People.Tel.
The correlation between the two variables
has dropped to 0.427, which reduces the r² value to 0.182. With this influential
observation removed, less that 20% of the variation in number of people per physician may be
explained by the number of people per television. Influential observations are also visible in the
new model, and their impact should also be investigated.
Residuals
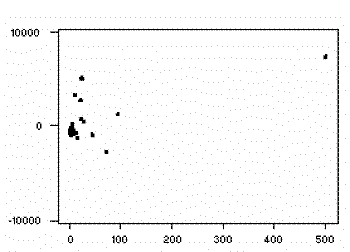 Once a regression model has been fit to a group
of data, examination of the residuals (the deviations from the fitted line to the observed values)
allows the modeler to investigate the validity of his or her assumption that a linear relationship
exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis
reveals any possible non-linear relationship among the variables, or might alert the modeler to
investigate lurking variables. In our example, the residual plot amplifies the
presence of outliers.
Once a regression model has been fit to a group
of data, examination of the residuals (the deviations from the fitted line to the observed values)
allows the modeler to investigate the validity of his or her assumption that a linear relationship
exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis
reveals any possible non-linear relationship among the variables, or might alert the modeler to
investigate lurking variables. In our example, the residual plot amplifies the
presence of outliers.
Lurking Variables
If non-linear trends are visible in the relationship between an explanatory and dependent variable,
there may be other influential variables to consider. A lurking variable
exists when the relationship between two variables is significantly affected by the presence of a
third variable which has not been included in the modeling effort. Since such a variable might be
a factor of time (for example, the effect of political or economic cycles), a time series plot
of the data is often a useful tool in identifying the presence of lurking variables.
Extrapolation
Whenever a linear regression model is fit to a group of data, the range of the data should be
carefully observed. Attempting to use a regression equation to predict values outside of
this range is often inappropriate, and may yield incredible answers. This practice is known as
extrapolation. Consider, for example, a linear model which relates weight gain
to age for young children. Applying such a model to adults, or even teenagers, would be absurd,
since the relationship between age and weight gain is not consistent for all age groups.
 To view the fit of the model to the observed data, one may plot the computed regression line over
the actual data points to evaluate the results. For this example, the plot appears to the right,
with number of individuals per television set (the explanatory variable) on the x-axis and number
of individuals per physician (the dependent variable) on the y-axis. While most of the data points
are clustered towards the lower left corner of the plot (indicating relatively few individuals
per television set and per physician), there are a few points which lie far away from the main
cluster of the data. These points are known as outliers, and depending on their
location may have a major impact on the regression line (see below).
To view the fit of the model to the observed data, one may plot the computed regression line over
the actual data points to evaluate the results. For this example, the plot appears to the right,
with number of individuals per television set (the explanatory variable) on the x-axis and number
of individuals per physician (the dependent variable) on the y-axis. While most of the data points
are clustered towards the lower left corner of the plot (indicating relatively few individuals
per television set and per physician), there are a few points which lie far away from the main
cluster of the data. These points are known as outliers, and depending on their
location may have a major impact on the regression line (see below).
 With this influential observation removed, the regression equation is
now
With this influential observation removed, the regression equation is
now  Once a regression model has been fit to a group
of data, examination of the residuals (the deviations from the fitted line to the observed values)
allows the modeler to investigate the validity of his or her assumption that a linear relationship
exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis
reveals any possible non-linear relationship among the variables, or might alert the modeler to
investigate lurking variables. In our example, the residual plot amplifies the
presence of outliers.
Once a regression model has been fit to a group
of data, examination of the residuals (the deviations from the fitted line to the observed values)
allows the modeler to investigate the validity of his or her assumption that a linear relationship
exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis
reveals any possible non-linear relationship among the variables, or might alert the modeler to
investigate lurking variables. In our example, the residual plot amplifies the
presence of outliers.