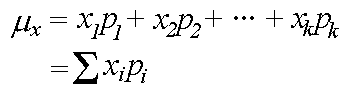
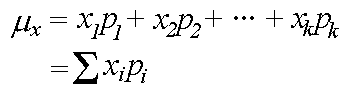
The mean of a random variable provides the long-run average of the variable, or the expected average outcome over many observations.
Outcome -$1.00 $0.00 $3.00 $5.00 Probability 0.30 0.40 0.20 0.10The mean outcome for this game is calculated as follows:
The law of large numbers states that the observed random mean
from an increasingly large number of observations of a random variable will
always approach the distribution mean
![]() . That is,
as the number of observations increases, the mean of these observations will
become closer and closer to the true mean of the random variable. This does
not imply, however, that short term averages will reflect the mean.
. That is,
as the number of observations increases, the mean of these observations will
become closer and closer to the true mean of the random variable. This does
not imply, however, that short term averages will reflect the mean.
In the above gambling example, suppose a woman plays the game five times, with the outcomes $0.00, -$1.00, $0.00, $0.00, -$1.00. She might assume, since the true mean of the random variable is $0.80, that she will win the next few games in order to "make up" for the fact that she has been losing. Unfortunately for her, this logic has no basis in probability theory. The law of large numbers does not apply for a short string of events, and her chances of winning the next game are no better than if she had won the previous game.
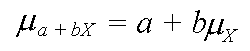
Outcome -$2.00 -$1.00 $2.00 $4.00 Probability 0.30 0.40 0.20 0.10The new mean is (-2*0.3) + (-1*0.4) + (2*0.2) + (4*0.1) = -0.6 + -0.4 + 0.4 + 0.4 = -0.2. This is equivalent to subtracting $1.00 from the original value of the mean, 0.8 -1.00 = -0.2. With the new payouts, the casino can expect to win 20 cents in the long run.
Suppose that the casino decides that the game does not have an impressive enough top prize with the lower payouts, and decides to double all of the prizes, as follows:
Outcome -$4.00 -$2.00 $4.00 $8.00 Probability 0.30 0.40 0.20 0.10Now the mean is (-4*0.3) + (-2*0.4) + (4*0.2) + (8*0.1) = -1.2 + -0.8 + 0.8 + 0.8 = -0.4. This is equivalent to multiplying the previous value of the mean by 2, increasing the expected winnings of the casino to 40 cents.
Overall, the difference between the original value of the mean (0.8) and the new value of the mean (-0.4) may be summarized by (0.8 - 1.0)*2 = -0.4.
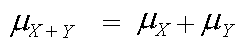
For example, suppose a casino offers one gambling game whose mean winnings are -$0.20 per play, and another game whose mean winnings are -$0.10 per play. Then the mean winnings for an individual simultaneously playing both games per play are -$0.20 + -$0.10 = -$0.30.

The standard deviation ![]() is
the square root of the variance.
is
the square root of the variance.
Outcome -$1.00 $0.00 $3.00 $5.00 Probability 0.30 0.40 0.20 0.10The variance for this distribution, with mean = 0.8, may be calculated as follows:

Since the spread of the distribution is not affected by adding or subtracting a constant, the value a is not considered. And, since the variance is a sum of squared terms, any multiplier value b must also be squared when adjusting the variance.
Outcome -$4.00 -$2.00 $4.00 $8.00 Probability 0.30 0.40 0.20 0.10The variance for this distribution, with mean = -0.4, may be calculated as follows:
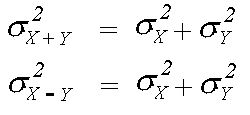
Variances are added for both the sum and difference of two independent random variables because the variation in each variable contributes to the variation in each case. If the variables are not independent, then variability in one variable is related to variability in the other. For this reason, the variance of their sum or difference may not be calculated using the above formula.
For example, suppose the amount of money (in dollars) a group of individuals spends on lunch is represented by variable X, and the amount of money the same group of individuals spends on dinner is represented by variable Y. The variance of the sum X + Y may not be calculated as the sum of the variances, since X and Y may not be considered as independent variables.