Source Degrees of Freedom Sum of squares Mean Square F
Model 1 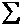 (
(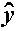 i-
i-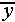 )² SSM/DFM MSM/MSE
Error n - 2
)² SSM/DFM MSM/MSE
Error n - 2 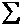 (yi-
(yi-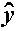 i)² SSE/DFE
i)² SSE/DFE
Total n - 1 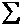 (yi-
(yi-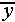 )² SST/DFT
)² SST/DFT
The "F" column provides a statistic for testing the hypothesis that
 1
1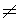 0
against the null hypothesis that
0
against the null hypothesis that  1 = 0.
The test statistic is the ratio MSM/MSE, the mean square model term divided
by the mean square error term. When the MSM term is large relative to
the MSE term, then the ratio is large and there is evidence against the
null hypothesis.
1 = 0.
The test statistic is the ratio MSM/MSE, the mean square model term divided
by the mean square error term. When the MSM term is large relative to
the MSE term, then the ratio is large and there is evidence against the
null hypothesis.
For simple linear regression, the statistic MSM/MSE has an
F distribution with degrees of freedom (DFM, DFE) =
(1, n - 2).
Example
The dataset "Healthy Breakfast" contains, among other variables,
the Consumer Reports ratings of 77 cereals and the number of grams
of sugar contained in each serving. (Data source: Free publication
available in many grocery stores. Dataset available through the
Statlib Data and Story
Library (DASL).)
Considering "Sugars" as the explanatory
variable and "Rating" as the response variable generated the following
regression line:
Rating = 59.3 - 2.40 Sugars (see Inference in
Linear Regression for more information about this example).
The "Analysis of Variance" portion of the MINITAB output is shown below.
The degrees of freedom are provided in the "DF" column, the calculated
sum of squares terms are provided in the "SS" column, and the mean
square terms are provided in the "MS" column.
Analysis of Variance
Source DF SS MS F P
Regression 1 8654.7 8654.7 102.35 0.000
Error 75 6342.1 84.6
Total 76 14996.8
In the ANOVA table for the "Healthy Breakfast" example, the F statistic
is equal to 8654.7/84.6 = 102.35. The distribution is F(1, 75),
and the probability of observing a value greater than or equal to 102.35
is less than 0.001. There is strong evidence that
 1 is not equal to zero.
1 is not equal to zero.
The r² term is equal to 0.577, indicating that 57.7% of the variability
in the response is explained by the explanatory variable.
ANOVA for Multiple Linear Regression
Multiple linear regression attempts to fit a regression line for
a response variable using more than one explanatory variable. The ANOVA calculations for
multiple regression are nearly identical to the calculations for simple linear regression,
except that the degrees of freedom are adjusted to reflect the number of explanatory variables
included in the model.
For p explanatory variables,
the model degrees of freedom (DFM) are equal to p, the error degrees of
freedom (DFE) are equal to (n - p - 1), and the total degrees of freedom
(DFT) are equal to (n - 1), the sum of DFM and DFE.
The corresponding ANOVA table is shown below:
Source Degrees of Freedom Sum of squares Mean Square F
Model p 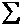 (
(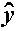 i-
i-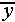 )² SSM/DFM MSM/MSE
Error n - p - 1
)² SSM/DFM MSM/MSE
Error n - p - 1 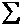 (yi-
(yi-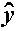 i)² SSE/DFE
i)² SSE/DFE
Total n - 1 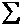 (yi-
(yi-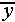 )² SST/DFT
)² SST/DFT
In multiple regression, the test statistic MSM/MSE has an F(p, n - p - 1)
distribution.
The null hypothesis states that  1 =
1 =
 2 = ... =
2 = ... =  p = 0,
and the alternative hypothesis simply states that at least one of the parameters
p = 0,
and the alternative hypothesis simply states that at least one of the parameters
 j
j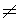 0, j = 1, 2, ,,, p.
Large values of the test statistic provide evidence against the null hypothesis.
0, j = 1, 2, ,,, p.
Large values of the test statistic provide evidence against the null hypothesis.
Note: The F test does not indicate which of the parameters  j
j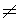 is not equal to zero, only that at least one of them is linearly related to the response variable.
is not equal to zero, only that at least one of them is linearly related to the response variable.
The ratio SSM/SST = R² is known as the squared multiple correlation
coefficient. This value is the proportion of the variation in the response variable
that is explained by the response variables. The square root of R² is called
the multiple correlation coefficient, the correlation between the observations
yi and the fitted values 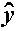 i.
i.
Example
The "Healthy Breakfast" dataset contains, among other variables,
the Consumer Reports ratings of 77 cereals, the number of grams
of sugar contained in each serving, and the number of grams of fat contained
in each serving. (Data source: Free publication
available in many grocery stores. Dataset available through the
Statlib Data and Story
Library (DASL).)
As a simple linear regression model, we previously considered "Sugars" as the explanatory
variable and "Rating" as the response variable. How do the ANOVA results change when "FAT"
is added as a second explanatory variable?
The regression line generated by the inclusion of "Sugars" and "Fat" is the following:
Rating = 61.1 - 2.21 Sugars - 3.07 Fat (see Multiple
Linear Regression for more information about this example).
The "Analysis of Variance" portion of the MINITAB output is shown below.
The degrees of freedom are provided in the "DF" column, the calculated
sum of squares terms are provided in the "SS" column, and the mean
square terms are provided in the "MS" column.
Analysis of Variance
Source DF SS MS F P
Regression 2 9325.3 4662.6 60.84 0.000
Error 74 5671.5 76.6
Total 76 14996.8
Source DF Seq SS
Sugars 1 8654.7
Fat 1 670.5
The mean square error term is smaller with "Fat" included, indicating less deviation between
the observed and fitted values. The P-value for the F test statistic is less than
0.001, providing strong evidence against the null hypothesis. The squared multiple correlation
R² = SSM/SST = 9325.3/14996.8 = 0.622, indicating that 62.2% of the variability
in the "Ratings" variable is explained by the "Sugars" and "Fat" variables. This is an improvement
over the simple linear model including only the "Sugars" variable.
RETURN TO MAIN PAGE.
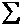 (yi -
(yi -
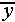 )²/(n - 1) = SST/DFT,
the total sum of squares divided by the total degrees of freedom (DFT).
)²/(n - 1) = SST/DFT,
the total sum of squares divided by the total degrees of freedom (DFT).
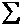 (
(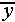 )²/(1) = SSM/DFM, since
the simple linear regression model has one explanatory variable x.
)²/(1) = SSM/DFM, since
the simple linear regression model has one explanatory variable x.
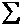 (yi -
(yi -
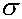 ²).
²).
 1
1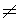 0
against the null hypothesis that
0
against the null hypothesis that