Multiple Linear Regression
Multiple linear regression attempts to model the relationship between
two or more explanatory variables and a response variable by fitting a linear
equation to observed data. Every value of the independent variable
x is associated with a value of the dependent variable y.
The population regression line for p explanatory variables x1,
x2, ... , xp is defined to be
 y
=
y
=  0 +
0 +  1x1 +
1x1 +
 2x2 + ... +
2x2 + ... +
 pxp. This line describes how the mean response
pxp. This line describes how the mean response
 y changes with the explanatory variables. The observed values for
y vary about their means
y changes with the explanatory variables. The observed values for
y vary about their means  y and are assumed
to have the same standard deviation
y and are assumed
to have the same standard deviation 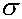 . The
fitted values b0, b1, ..., bp
estimate the parameters
. The
fitted values b0, b1, ..., bp
estimate the parameters  0,
0,  1,
...,
1,
...,  p of the population regression line.
p of the population regression line.
Since the observed values for y vary about their means  y,
the multiple regression model includes a term for this variation. In words, the model is expressed
as DATA = FIT + RESIDUAL, where the "FIT" term represents the expression
y,
the multiple regression model includes a term for this variation. In words, the model is expressed
as DATA = FIT + RESIDUAL, where the "FIT" term represents the expression  0 +
0 +
 1x1 +
1x1 +
 2x2 + ...
2x2 + ...
 pxp.
The "RESIDUAL" term represents the deviations of the observed values y from their
means
pxp.
The "RESIDUAL" term represents the deviations of the observed values y from their
means  y, which are normally distributed with mean
0 and variance
y, which are normally distributed with mean
0 and variance 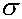 . The notation for the model deviations is
. The notation for the model deviations is
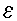 .
.
Formally, the model for multiple linear regression, given n observations, is
yi =  0 +
0 +
 1xi1 +
1xi1 +
 2xi2 + ...
2xi2 + ...
 pxip +
pxip +
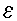 i for i = 1,2, ... n.
i for i = 1,2, ... n.
In the least-squares model, the best-fitting line for the observed data is calculated by
minimizing the sum of the squares of the
vertical deviations from each data point to the line (if a point lies on the fitted line exactly,
then its vertical deviation is 0). Because the deviations are first squared, then summed, there
are no cancellations between positive and negative values. The least-squares estimates
b0, b1, ... bp are usually computed
by statistical software.
The values fit by the equation b0 + b1xi1 +
... + bpxip are denoted 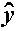 i, and the residuals ei are equal to yi -
i, and the residuals ei are equal to yi -
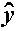 i, the difference between the observed and fitted values.
The sum of the residuals is equal to zero.
i, the difference between the observed and fitted values.
The sum of the residuals is equal to zero.
The variance 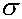 ² may be estimated by s² =
² may be estimated by s² =
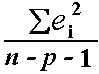 , also known as the mean-squared error (or MSE).
, also known as the mean-squared error (or MSE).
The estimate of
the standard error s is the square root of the MSE.
Example
The dataset "Healthy Breakfast" contains, among other variables,
the Consumer Reports ratings of 77 cereals and the number of grams of sugar contained
in each serving. (Data source: Free publication available in many grocery stores.
Dataset available through the Statlib Data and Story Library (DASL).)
A simple linear regression model considering "Sugars" as the explanatory variable and "Rating"
as the response variable produced the regression line
Rating = 59.3 - 2.40 Sugars, with the square of the correlation
r² = 0.577 (see Inference in Linear Regression for more
details on this regression).
The "Healthy Breakfast" dataset includes several other variables, including grams of fat per serving and
grams of dietary fiber per serving. Is the model significantly
improved when these variables are included?
Suppose we are first interested in adding the "Fat" variable. The correlation between "Fat"
and "Rating" is equal to -0.409, while the correlation between "Sugars" and "Fat" is equal to
0.271. Since "Fat" and "Sugar" are not highly correlated, the addition of the "Fat" variable
may significantly improve the model.
The MINITAB "Regress" command produced the following results:
Regression Analysis
The regression equation is
Rating = 61.1 - 3.07 Fat - 2.21 Sugars
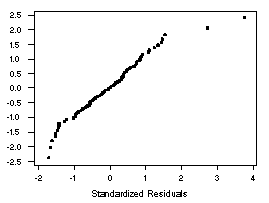
After fitting the regression line, it is important to investigate the residuals to determine
whether or not they appear to fit the assumption of a normal distribution. A
normal quantile plot of the
standardized residuals y - 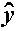 is shown to the left.
Despite two large values which may be outliers in the data, the residuals do not seem to deviate
from a random sample from a normal distribution in any systematic manner.
is shown to the left.
Despite two large values which may be outliers in the data, the residuals do not seem to deviate
from a random sample from a normal distribution in any systematic manner.
The MINITAB output provides a great deal of information. Under the equation for the
regression line, the output provides the least-squares estimates for each parameter, listed
in the "Coef" column next to the variable to which it corresponds.
The calculated standard deviations are provided in the second column.
Predictor Coef StDev T P
Constant 61.089 1.953 31.28 0.000
Fat -3.066 1.036 -2.96 0.004
Sugars -2.2128 0.2347 -9.43 0.000
S = 8.755 R-Sq = 62.2% R-Sq(adj) = 61.2%
Significance Tests
The third column "T" of the MINITAB "REGRESS" output provides test statistics.
As in linear regression, one wishes to test the
significance of the parameters included. For any of the variables xj
included in a multiple regression model, the null hypothesis states that the coefficient
 j is equal to 0.
The alternative hypothesis may be one-sided or two-sided, stating
that
j is equal to 0.
The alternative hypothesis may be one-sided or two-sided, stating
that  j
is either less than 0, greater than 0, or simply not equal to 0.
j
is either less than 0, greater than 0, or simply not equal to 0.
The test statistic t is equal to bj/sbj,
the parameter estimate divided by its standard deviation.
This value follows a t(n-p-1) distribution when p variables are included in
the model.
In the example above, the parameter estimate for the "Fat" variable is -3.066 with
standard deviation 1.036 The test statistic is t = -3.066/1.036 = -2.96,
provided in the "T" column of the MINITAB output. For a two-sided test, the probability
of interest is 2P(T>|-2.96|) for the t(77-2-1) = t(74) distribution,
which is about 0.004. The "P" column of the MINITAB output provides the P-value
associated with the two-sided test. Since the P-values for both "Fat" and "Sugar" are
highly significant, both variables may be included in the model.
Condidence Intervals for Regression Parameters
A level C confidence interval for the parameter  j
may be computed from the estimate bj using the
computed standard deviations and the appropriate critical value t* from
the t(n-p-1) distribution. The confidence interval for
j
may be computed from the estimate bj using the
computed standard deviations and the appropriate critical value t* from
the t(n-p-1) distribution. The confidence interval for
 j takes the form
bj + t*sbj.
j takes the form
bj + t*sbj.
Continuing with the "Healthy Breakfast" example, suppose we choose to
add the "Fiber" variable to our model. The MINITAB results are the following:
Regression Analysis
The regression equation is
Rating = 53.4 - 3.48 Fat + 2.95 Fiber - 1.96 Sugars
Predictor Coef StDev T P
Constant 53.437 1.342 39.82 0.000
Fat -3.4802 0.6209 -5.61 0.000
Fiber 2.9503 0.2549 11.57 0.000
Sugars -1.9640 0.1420 -13.83 0.000
S = 5.235 R-Sq = 86.7% R-Sq(adj) = 86.1%
The squared multiple correlation R² is now equal to 0.861, and all of the
variables are significant by the t tests. Examination of the residuals indicates
no unusual patterns. The inclusion of the "Fat," "Fiber," and "Sugars" variables
explains 86.7% of the variability of the data, a significant improvement over the smaller models.
For additional tests and a continuation of this example, see ANOVA
for Multiple Linear Regression.
RETURN TO MAIN PAGE.
 y,
the multiple regression model includes a term for this variation. In words, the model is expressed
as DATA = FIT + RESIDUAL, where the "FIT" term represents the expression
y,
the multiple regression model includes a term for this variation. In words, the model is expressed
as DATA = FIT + RESIDUAL, where the "FIT" term represents the expression  0 +
0 +
 1x1 +
1x1 +
 2x2 + ...
2x2 + ...
 pxp.
The "RESIDUAL" term represents the deviations of the observed values y from their
means
pxp.
The "RESIDUAL" term represents the deviations of the observed values y from their
means  y, which are normally distributed with mean
0 and variance
y, which are normally distributed with mean
0 and variance 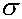 . The notation for the model deviations is
. The notation for the model deviations is
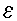 .
.
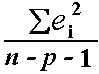 , also known as the mean-squared error (or MSE).
, also known as the mean-squared error (or MSE).
