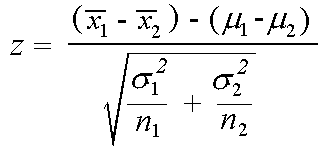
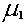 -
- 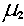 )
(the difference between the two population means) which would not be
rejected in the two-sided hypothesis test of
)
(the difference between the two population means) which would not be
rejected in the two-sided hypothesis test of
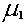 =
=
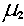 against
Ha:
against
Ha: 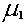
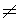
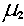 , i.e.
, i.e.
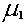 -
- 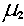 = 0 against
Ha:
= 0 against
Ha: 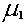 -
-
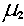
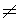 0.
0.
If the confidence interval includes 0 we can say that there is no significant difference between the means of the two populations, at a given level of confidence.
(Definition taken from Valerie J. Easton and John H. McColl's Statistics Glossary v1.1)
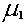 and
and 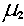 and
known standard deviations
and
known standard deviations 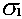 and
and
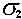 , the test statistic comparing the means is known as
the two-sample z statistic
, the test statistic comparing the means is known as
the two-sample z statistic
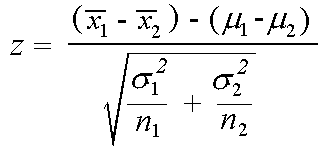
The null hypothesis always assumes that the means are equal, while the alternative hypothesis may be one-sided or two-sided.
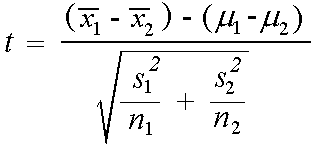
The confidence interval for the difference in means 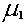 -
-
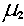 is given by
where t* is the upper (1-C)/2 critical value for the t distribution
with k degrees of freedom (with k equal to either the smaller of n1-1 and
n1-2 or the calculated degrees of freedom).
is given by
where t* is the upper (1-C)/2 critical value for the t distribution
with k degrees of freedom (with k equal to either the smaller of n1-1 and
n1-2 or the calculated degrees of freedom).
Descriptive Statistics
Variable C2 N Mean Median Tr Mean StDev SE Mean
C1 1 65 98.105 98.100 98.114 0.699 0.087
2 65 98.394 98.400 98.390 0.743 0.092
Variable C2 Min Max Q1 Q3
C1 1 96.300 99.500 97.600 98.600
2 96.400 100.800 98.000 98.800
Is there a significant difference between the mean body temperatures for men and women?
To test H0: 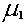 -
- 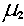 = 0 against
Ha:
= 0 against
Ha: 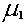 -
-
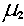
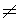 0,
compute the test statistic (98.105 - 98.394)/(sqrt(0.699²/65 + 0.743²/65))
= -0.289/0.127 = -2.276. Using the t(64) distribution, estimated in Table E in Moore
and McCabe by the t(60) distribution, we see that 2P(t>2.276) is between 0.04 and 0.02, indicating
a significant difference between the means at the 0.05 level (although not at the 0.01 level).
0,
compute the test statistic (98.105 - 98.394)/(sqrt(0.699²/65 + 0.743²/65))
= -0.289/0.127 = -2.276. Using the t(64) distribution, estimated in Table E in Moore
and McCabe by the t(60) distribution, we see that 2P(t>2.276) is between 0.04 and 0.02, indicating
a significant difference between the means at the 0.05 level (although not at the 0.01 level).
To compute a 95% confidence interval, we first note that the 0.025 critical value t* for the t(60) distribution is 2.000, giving the interval ((98.105 - 98.394) + 2.000*0.127) = (-0.289 - 0.254, -0.289 + 0.254) = (-0.543, -0.045). The value 0 is not included in the interval, again indicating a significant difference at the 0.05 level.
Performing this test in MINITAB using the "TWOT" command gives the results
Two Sample T-Test and Confidence Interval Two sample T for C1 C2 N Mean StDev SE Mean 1 65 98.105 0.699 0.087 2 65 98.394 0.743 0.092 95% CI for mu (1) - mu (2): ( -0.540, -0.039) T-Test mu (1) = mu (2) (vs not =): T= -2.29 P=0.024 DF= 127Although the MINITAB calculated degrees of freedom (127) are much higher than the conservative estimate of 64, we see that the results are much the same.
Data source: Data presented in Mackowiak, P.A., Wasserman, S.S., and Levine, M.M. (1992), "A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and Other Legacies of Carl Reinhold August Wunderlich," Journal of the American Medical Association, 268, 1578-1580. Dataset available through the JSE Dataset Archive.
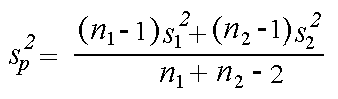
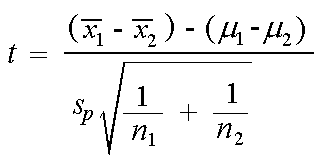
Two Sample T-Test and Confidence Interval Two sample T for C1 C2 N Mean StDev SE Mean 1 65 98.105 0.699 0.087 2 65 98.394 0.743 0.092 95% CI for mu (1) - mu (2): ( -0.540, -0.039) T-Test mu (1) = mu (2) (vs not =): T= -2.29 P=0.024 DF= 128 Both use Pooled StDev = 0.721The test results were nearly identical in this case.