Tests of Significance
Once sample data has been gathered through an observational study or
experiment, statistical inference allows analysts to assess evidence in
favor or some claim about the population from which the sample has been
drawn. The methods of inference used to support or reject claims based on
sample data are known as tests of significance.
Every test of significance begins with a null hypothesis H0.
H0 represents a theory that has been put forward, either because
it is believed to be true or because it is to be used as a basis for argument, but
has not been proved. For example, in a clinical trial of a new drug, the null
hypothesis might be that the new drug is no better, on average, than the current drug. We
would write H0: there is no difference between the two drugs on average.
The alternative hypothesis, Ha, is a statement of what a statistical
hypothesis test is set up to establish. For example, in a clinical trial of a new drug,
the alternative hypothesis might be that the new drug has a different effect, on average,
compared to that of the current drug. We would write Ha: the two drugs have
different effects, on average. The alternative hypothesis might also be that the new drug
is better, on average, than the current drug. In this case we would write Ha:
the new drug is better than the current drug, on average.
The final conclusion once the test has been carried out is always given in terms of the null
hypothesis. We either "reject H0 in favor of Ha" or
"do not reject H0"; we never conclude "reject Ha",
or even "accept Ha".
If we conclude "do not reject H0", this does not necessarily mean that the null
hypothesis is true, it only suggests that there is not sufficient evidence against
H0 in favor of Ha; rejecting the null hypothesis then,
suggests that the alternative hypothesis may be true.
(Definitions taken from Valerie J. Easton and John H. McColl's
Statistics Glossary v1.1)
Hypotheses are always stated in terms of population parameter, such as the mean
 .
An alternative hypothesis may be one-sided or two-sided.
A one-sided hypothesis claims that a parameter is either larger or smaller than the
value given by the null hypothesis. A two-sided hypothesis claims that a parameter is simply
not equal to the value given by the null hypothesis -- the direction does not matter.
.
An alternative hypothesis may be one-sided or two-sided.
A one-sided hypothesis claims that a parameter is either larger or smaller than the
value given by the null hypothesis. A two-sided hypothesis claims that a parameter is simply
not equal to the value given by the null hypothesis -- the direction does not matter.
Hypotheses for a one-sided test for a population mean take the following form:
H0: = k
= k
Ha: > k
> k
or
H0: = k
= k
Ha: < k.
< k.
Hypotheses for a two-sided test for a population mean take the following form:
H0: = k
= k
Ha:
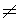 k.
k.
A confidence interval gives an estimated range of values
which is likely to include an unknown population parameter, the estimated
range being calculated from a given set of sample data.
(Definition taken from Valerie J. Easton and John H. McColl's
Statistics Glossary v1.1)
Example
Suppose a test has been given to all high school students in a certain state. The mean test score
for the entire state is 70, with standard deviation equal to 10. Members of the school board
suspect that female students have a higher mean score on the test than male students, because the
mean score 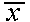 from a random sample of 64 female students
is equal to 73. Does this provide strong evidence that the overall mean for female students is
higher?
from a random sample of 64 female students
is equal to 73. Does this provide strong evidence that the overall mean for female students is
higher?
The null hypothesis H0 claims that there is no difference between the mean
score for female students and the mean for the entire population, so that
 = 70. The alternative hypothesis claims that the mean for
female students is higher than the entire student population mean, so that
= 70. The alternative hypothesis claims that the mean for
female students is higher than the entire student population mean, so that
 > 70.
> 70.
Significance Tests for Unknown Mean and Known Standard Deviation
Once null and alternative hypotheses have been formulated for a particular claim, the next step
is to compute a test statistic. For claims about a population mean from a
population with a normal distribution or for any sample with large sample
size n (for which the sample mean will follow a normal distribution by the
Central Limit Theorem), if the standard deviation 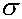 is
known, the appropriate significance test is known as the z-test, where the test
statistic is defined as z =
is
known, the appropriate significance test is known as the z-test, where the test
statistic is defined as z = 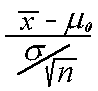 .
.
The test statistic follows the standard normal distribution (with mean = 0 and standard deviation
= 1). The test statistic z is used to compute the
P-value for the standard normal distribution, the probability that a value at least as
extreme as the test statistic would be observed under the null hypothesis. Given the null
hypothesis that the population mean  is equal to a given
value
is equal to a given
value  0, the P-values for testing H0
against each of the possible alternative hypotheses are:
0, the P-values for testing H0
against each of the possible alternative hypotheses are:
P(Z > z) for Ha: >
>
 0
0
P(Z < z) for Ha: <
<
 0
0
2P(Z>|z|) for Ha:
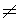
 0.
0.
The probability is doubled for the two-sided test, since the two-sided alternative hypothesis
considers the possibility of observing extreme values on either tail of the normal
distribution.
Example
In the test score example above, where the sample mean equals 73 and the population standard
deviation is equal to 10, the test statistic is computed as follows:
z = (73 - 70)/(10/sqrt(64)) = 3/1.25 = 2.4. Since this is a one-sided test, the P-value
is equal to the probability that of observing a value greater than 2.4 in the standard normal
distribution, or P(Z > 2.4) = 1 - P(Z < 2.4) = 1 - 0.9918 = 0.0082. The
P-value is less than 0.01, indicating that it is highly unlikely that these results would
be observed under the null hypothesis. The school board can confidently reject
H0 given this result, although they cannot conclude any additional
information about the mean of the distribution.
Significance Levels
The significance level 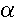 for a given hypothesis
test is a value for which a P-value less than or equal to
for a given hypothesis
test is a value for which a P-value less than or equal to 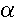 is considered statistically significant. Typical values for
is considered statistically significant. Typical values for 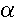 are 0.1, 0.05, and 0.01. These values correspond to the probability of observing such an extreme
value by chance. In the test score example above, the P-value is 0.0082, so the probability of
observing such a value by chance is less that 0.01, and the result is significant at the
0.01 level.
are 0.1, 0.05, and 0.01. These values correspond to the probability of observing such an extreme
value by chance. In the test score example above, the P-value is 0.0082, so the probability of
observing such a value by chance is less that 0.01, and the result is significant at the
0.01 level.
In a one-sided test, 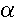 corresponds to the critical value
z* such that P(Z > z*) =
corresponds to the critical value
z* such that P(Z > z*) = 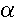 .
For example, if the desired significance level for a result is 0.05, the corresponding value
for z must be greater than or equal to z* = 1.645
(or less than or equal to -1.645 for a one-sided alternative claiming that the mean is
less than the null hypothesis).
For a two-sided test, we are interested in the probability that
2P(Z > z*) =
.
For example, if the desired significance level for a result is 0.05, the corresponding value
for z must be greater than or equal to z* = 1.645
(or less than or equal to -1.645 for a one-sided alternative claiming that the mean is
less than the null hypothesis).
For a two-sided test, we are interested in the probability that
2P(Z > z*) = 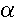 , so the
critical value z* corresponds to the
, so the
critical value z* corresponds to the 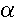 /2
significance level. To achieve a significance level of 0.05 for a two-sided test,
the absolute value of the test statistic (|z|) must be greater than or equal to
the critical value 1.96 (which corresponds to the level 0.025 for a one-sided test).
/2
significance level. To achieve a significance level of 0.05 for a two-sided test,
the absolute value of the test statistic (|z|) must be greater than or equal to
the critical value 1.96 (which corresponds to the level 0.025 for a one-sided test).
Another interpretation of the significance level 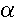 ,
based in decision theory, is that
,
based in decision theory, is that 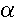 corresponds
to the value for which one chooses to reject or accept the null hypothesis
H0. In the above example, the value 0.0082 would result in rejection of the
null hypothesis at the 0.01 level. The probability that this is a mistake -- that, in fact,
the null hypothesis is true given the z-statistic -- is less than 0.01. In decision theory,
this is known as a Type I error. The probability of a Type I error is equal to
the significance level
corresponds
to the value for which one chooses to reject or accept the null hypothesis
H0. In the above example, the value 0.0082 would result in rejection of the
null hypothesis at the 0.01 level. The probability that this is a mistake -- that, in fact,
the null hypothesis is true given the z-statistic -- is less than 0.01. In decision theory,
this is known as a Type I error. The probability of a Type I error is equal to
the significance level 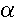 , and the probability of rejecting
the null hypothesis when it is in fact false (a correct decision) is equal to
1 -
, and the probability of rejecting
the null hypothesis when it is in fact false (a correct decision) is equal to
1 - 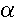 . To minimize the probability of Type I error, the significance
level is generally chosen to be small.
. To minimize the probability of Type I error, the significance
level is generally chosen to be small.
Example
Of all of the individuals who develop a certain rash, suppose the mean recovery time for
individuals who do not use any form of treatment is 30 days with standard deviation equal to 8.
A pharmaceutical company manufacturing a certain cream wishes to determine whether the cream
shortens, extends, or has no effect on the recovery time. The company chooses a random sample
of 100 individuals who have used the cream, and determines that the mean recovery time for
these individuals was 28.5 days. Does the cream have any effect?
Since the pharmaceutical company is interested in any difference from the mean recovery
time for all individuals, the alternative hypothesis Ha is two-sided:

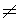 30. The test statistic is calculated
to be z = (28.5 - 30)/(8/sqrt(100)) = -1.5/0.8 = -1.875. The P-value for
this statistic is 2P(Z > 1.875) = 2(1 - P((Z < 1.875) = 2(1- 0.9693)
= 2(0.0307) = 0.0614. This is not significant at the 0.05 level, although it is significant
at the 0.1 level.
30. The test statistic is calculated
to be z = (28.5 - 30)/(8/sqrt(100)) = -1.5/0.8 = -1.875. The P-value for
this statistic is 2P(Z > 1.875) = 2(1 - P((Z < 1.875) = 2(1- 0.9693)
= 2(0.0307) = 0.0614. This is not significant at the 0.05 level, although it is significant
at the 0.1 level.
Decision theory is also concerned with a second error possible in significance testing,
known as Type II error. Contrary to Type I error, Type II error is the
error made when the null hypothesis is incorrectly accepted. The probability of correctly
rejecting the null hypothesis when it is false, the complement of the Type II error, is known as
the power of a test. Formally defined, the power of a test is the
probability that a fixed level 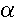 significance test will reject
the null hypothesis H0 when a particular alternative value of the
parameter is true.
significance test will reject
the null hypothesis H0 when a particular alternative value of the
parameter is true.
Example
In the test score example, for a fixed significance level of 0.10, suppose the school board
wishes to be able to reject the null hypothesis (that the mean = 70) if the mean for female
students is in fact 72. To determine the power of the test against this alternative, first
note that the critical value for rejecting the null hypothesis is z* = 1.282.
The calculated value for z will be greater than 1.282 whenever
(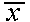 - 70)/(1.25) > 1.282, or
- 70)/(1.25) > 1.282, or
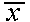 > 71.6.
The probability of rejecting the null hypothesis (mean = 70) given that the alternative
hypotheses (mean = 72) is true is calculated by:
> 71.6.
The probability of rejecting the null hypothesis (mean = 70) given that the alternative
hypotheses (mean = 72) is true is calculated by:
P((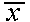 > 71.6 |
> 71.6 |  = 72)
= 72)
= P((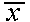 - 72)/(1.25) > (71.6 - 72)/1.25)
- 72)/(1.25) > (71.6 - 72)/1.25)
= P(Z > -0.32) = 1 - P(Z < -0.32) = 1 - 0.3745 = 0.6255.
The power is about 0.60, indicating that although the test is more likely than not to reject the
null hypothesis for this value, the probability of a Type II error is high.
Significance Tests for Unknown Mean and Unknown Standard Deviation
In most practical research, the standard deviation for the population of interest is not known.
In this case, the standard deviation 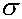 is replaced by
the estimated standard deviation s, also known as
the standard error. Since the standard error is an estimate for the true value of
the standard deviation, the distribution of the sample mean
is replaced by
the estimated standard deviation s, also known as
the standard error. Since the standard error is an estimate for the true value of
the standard deviation, the distribution of the sample mean
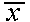 is no longer normal with mean
is no longer normal with mean  and standard deviation
and standard deviation
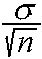 . Instead, the sample mean follows the
t distribution with mean
. Instead, the sample mean follows the
t distribution with mean  and standard deviation
and standard deviation
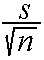 . The t distribution is also described by
its degrees of freedom. For a sample of size n, the t distribution
will have n-1 degrees of freedom. The notation for a
t distribution with k degrees of freedom is t(k). As the sample size n
increases, the t distribution becomes closer to the normal distribution, since the standard
error approaches the true standard deviation
. The t distribution is also described by
its degrees of freedom. For a sample of size n, the t distribution
will have n-1 degrees of freedom. The notation for a
t distribution with k degrees of freedom is t(k). As the sample size n
increases, the t distribution becomes closer to the normal distribution, since the standard
error approaches the true standard deviation 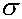 for large n.
for large n.
For claims about a population mean from a population with a normal
distribution or for any sample with large sample
size n (for which the sample mean will follow a normal distribution by the
Central Limit Theorem) with unknown standard deviation,
the appropriate significance test is known as the t-test, where the test
statistic is defined as t = 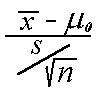 .
.
The test statistic follows the t distribution with n-1 degrees of freedom.
The test statistic z is used to compute the
P-value for the t distribution, the probability that a value at least as
extreme as the test statistic would be observed under the null hypothesis.
Example
The dataset "Normal Body Temperature, Gender, and Heart Rate" contains 130 observations of
body temperature, along with the gender of each individual and his or her heart rate. Using
the MINITAB "DESCRIBE" command provides the following information:
Descriptive Statistics
Variable N Mean Median Tr Mean StDev SE Mean
TEMP 130 98.249 98.300 98.253 0.733 0.064
Variable Min Max Q1 Q3
TEMP 96.300 100.800 97.800 98.700
Since the normal body temperature is generally assumed to be 98.6 degrees Fahrenheit, one can use
the data to test the following one-sided hypothesis:
H0: = 98.6 vs
= 98.6 vs
Ha: < 98.6.
< 98.6.
The t test statistic is equal to (98.249 - 98.6)/0.064 = -0.351/0.064 = -5.48.
P(t< -5.48) = P(t> 5.48). The t distribution with
129 degrees of freedom may be approximated by the t distribution with 100 degrees
of freedom (found in Table E in Moore and McCabe), where P(t> 5.48) is
less than 0.0005. This result is significant at the 0.01 level and beyond, indicating that
the null hypotheses can be rejected with confidence.
To perform this t-test in MINITAB, the "TTEST" command with the "ALTERNATIVE" subcommand
may be applied as follows:
MTB > ttest mu = 98.6 c1;
SUBC > alt= -1.
T-Test of the Mean
Test of mu = 98.6000 vs mu < 98.6000
Variable N Mean StDev SE Mean T P
TEMP 130 98.2492 0.7332 0.0643 -5.45 0.0000
These results represents the exact calculations for the t(129) distribution.
Data source: Data presented in Mackowiak, P.A., Wasserman, S.S., and Levine, M.M. (1992),
"A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and
Other Legacies of Carl Reinhold August Wunderlich," Journal of the American Medical
Association, 268, 1578-1580. Dataset available through the
JSE Dataset Archive.
Matched Pairs
In many experiments, one wishes to compare measurements from two populations.
This is common in medical studies involving control groups, for example,
as well as in studies requiring before-and-after measurements. Such
studies have a matched pairs design, where the
difference between the two measurements in each pair is the
parameter of interest.
Analysis of data from a matched pairs experiment compares the two measurements
by subtracting one from the other and basing test hypotheses upon the
differences. Usually, the null hypothesis H0 assumes
that that the mean of these differences is equal to 0, while the alternative
hypothesis Ha claims that the mean of the differences
is not equal to zero (the alternative hypothesis may be one- or two-sided,
depending on the experiment). Using the differences between the paired
measurements as single observations, the standard t procedures with
n-1 degrees of freedom are followed as above.
Example
In the "Helium Football" experiment, a punter was given two footballs to
kick, one filled with air and the other filled with helium. The punter was
unaware of the difference between the balls, and was asked to kick each ball
39 times. The balls were alternated for each kick, so each of the 39 trials
contains one measurement for the air-filled ball and one measurement for
the helium-filled ball. Given that the conditions (leg fatigue, etc.)
were basically the same for each kick within a trial, a matched pairs analysis
of the trials is appropriate. Is there evidence that the helium-filled ball
improved the kicker's performance?
In MINITAB, subtracting the air-filled measurement from the helium-filled measurement for each
trial and applying the "DESCRIBE" command to the resulting differences gives the following
results:
Descriptive Statistics
Variable N Mean Median Tr Mean StDev SE Mean
Hel. - Air 39 0.46 1.00 0.40 6.87 1.10
Variable Min Max Q1 Q3
Hel. - Air -14.00 17.00 -2.00 4.00
Using MINITAB to perform a t-test of the null hypothesis H0:
 = 0 vs
Ha:
= 0 vs
Ha: > 0
gives the following analysis:
> 0
gives the following analysis:
T-Test of the Mean
Test of mu = 0.00 vs mu > 0.00
Variable N Mean StDev SE Mean T P
Hel. - A 39 0.46 6.87 1.10 0.42 0.34
The P-Value of 0.34 indicates that this result is not significant at any acceptable
level. A 95% confidence interval for the t-distribution
with 38 degrees of freedom for the difference in measurements is (-1.76, 2.69), computed
using the MINITAB "TINTERVAL" command.
Data source: Lafferty, M.B. (1993), "OSU scientists get a kick out of sports controversy,"
The Columbus Dispatch (November 21, 1993), B7. Dataset available through the
Statlib Data and Story Library (DASL).
The Sign Test
Another method of analysis for matched pairs data is a distribution-free test known
as the sign test. This test does not require any normality assumptions about the
data, and simply involves counting the number of positive differences between the matched pairs
and relating these to a binomial distribution. The concept behind the
sign test reasons that if there is no true difference, then the probability of
observing an increase in each pair is equal to the probability of observing a decrease in
each pair: p = 1/2. Assuming each pair is independent, the null hypothesis follows the
distribution B(n,1/2), where n is the number of pairs where some difference
is observed.
To perform a sign test on matched pairs data, take the difference between the two measurements
in each pair and count the number of non-zero differences n. Of these, count the number
of positive differences X. Determine the probability of observing X positive
differences for a B(n,1/2) distribution, and use this probability as a P-value
for the null hypothesis.
Example
In the "Helium Football" example above, 2 of the 39 trials recorded no difference between
kicks for the air-filled and helium-filled balls. Of the remaining 37 trials, 20 recorded
a positive difference between the two kicks. Under the null hypothesis, p = 1/2, the
differences would follow the B(37,1/2) distribution. The probability of observing 20
or more positive differences, P(X>20) = 1 - P(X<19) =
1 - 0.6286 = 0.3714. This value indicates that there is not strong evidence against the null
hypothesis, as observed previously with the t-test.
RETURN TO MAIN PAGE.
 .
An alternative hypothesis may be one-sided or two-sided.
A one-sided hypothesis claims that a parameter is either larger or smaller than the
value given by the null hypothesis. A two-sided hypothesis claims that a parameter is simply
not equal to the value given by the null hypothesis -- the direction does not matter.
.
An alternative hypothesis may be one-sided or two-sided.
A one-sided hypothesis claims that a parameter is either larger or smaller than the
value given by the null hypothesis. A two-sided hypothesis claims that a parameter is simply
not equal to the value given by the null hypothesis -- the direction does not matter.
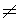 k.
k.
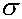 is
known, the appropriate significance test is known as the z-test, where the test
statistic is defined as z =
is
known, the appropriate significance test is known as the z-test, where the test
statistic is defined as z = 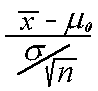 .
.
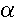 for a given hypothesis
test is a value for which a P-value less than or equal to
for a given hypothesis
test is a value for which a P-value less than or equal to 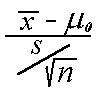 .
.